点评2:李教授(某985高校电子工程系博导)
"作为教学参考,这篇文章清晰易懂,但若能加入更多数学推导(如传递函数分析),会更适合研究生阶段的学习。"
点评3:王技术总监(某音频设备公司研发负责人)
"实战案例部分非常实用!我们在开发高端音频DSP时,正是采用类似方法优化带通滤波器。期待作者后续探讨数字滤波器的实现方式。"
通过本文,相信读者已经对有源带通滤波器有了系统认识。无论是初学者还是资深工程师,都能从中找到有价值的设计思路。未来,随着集成电路技术的发展,有源滤波器将在5G、物联网等领域发挥更大作用,值得我们持续关注!

PCB布局优化:
1. 什么是有源带通滤波器?
有源带通滤波器是一种仅允许特定频率范围(通带)信号通过,同时抑制低频和高频成分的电子电路。其核心在于结合了**低通滤波器(LPF)和高通滤波器(HPF)**的特性,并利用运算放大器(Op-Amp)提供增益,以弥补信号在传输过程中的损耗。
关键参数解析
- 中心频率(f₀):通带的中心点,通常由电阻和电容决定。
- 带宽(BW):通带的频率范围,BW = f₂ - f₁(f₂和f₁分别为上、下截止频率)。
- 品质因数(Q):衡量滤波器选择性,Q = f₀ / BW,Q值越高,通带越窄,选择性越强。
2. 有源带通滤波器的经典拓扑结构
有源带通滤波器主要有两种实现方式:多重反馈型(MFB)和状态变量型(Sallen-Key),它们各有优劣,适用于不同场景。
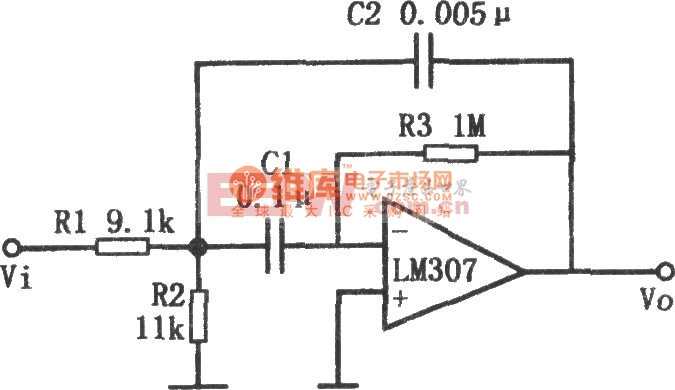
(1)多重反馈型(MFB)带通滤波器
- 优点:结构简单,仅需一个运算放大器,适合中低Q值应用。
- 缺点:Q值过高时,元件参数敏感,稳定性下降。
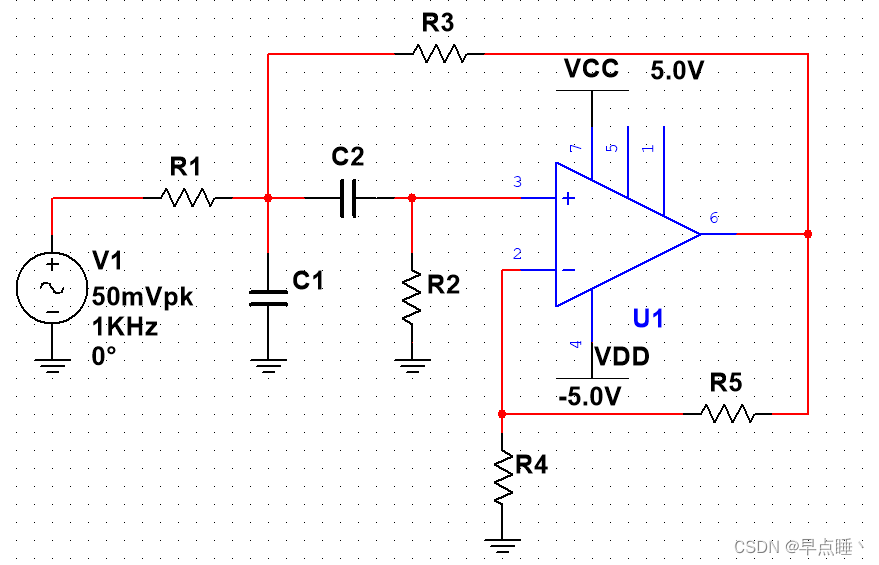
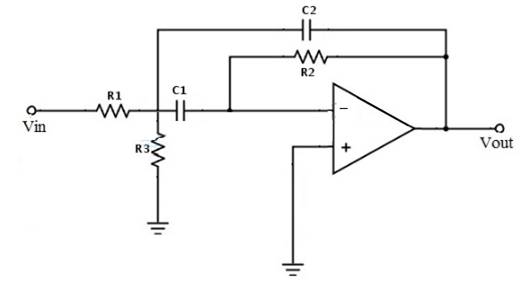
(图:MFB带通滤波器典型电路)
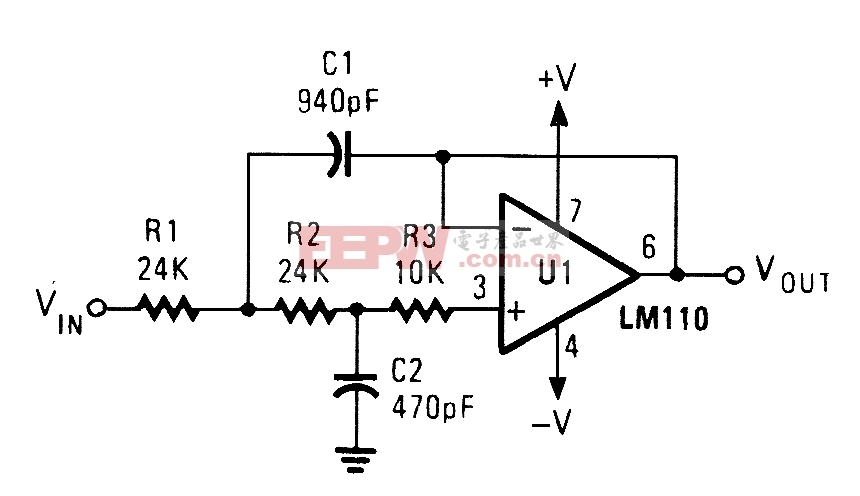
(2)状态变量型带通滤波器
- 优点:可独立调节中心频率和Q值,适合高Q值需求。
- 缺点:需要多个运算放大器,电路较复杂。
3. 实际设计案例:如何搭建一个中心频率1kHz的带通滤波器?
假设我们需要设计一个中心频率1kHz、Q=5的MFB带通滤波器,步骤如下:
-
确定元件值:
- 缩短信号走线,降低寄生电容影响。
- 采用低噪声运放(如OPA2134)以减少热噪声干扰。
4. 高阶应用:如何优化滤波器性能?
- 提高选择性:采用级联设计,如两个二阶滤波器串联,形成四阶带通滤波器,使滚降更陡峭。
- 降低噪声:选择低噪声运放,并优化电源去耦(如并联0.1μF和10μF电容)。
- 自动调谐:结合数字电位器或MCU控制,实现动态频率调整,适应不同信号环境。
5. 行业应用:有源带通滤波器在哪里大显身手?
- 无线通信:用于提取特定频段信号(如FM收音机的中频滤波)。
- 生物医学:ECG信号处理,滤除50/60Hz工频干扰。
- 音频工程:均衡器设计,增强特定频段音效。
【资深点评】业界专家如何看待本文?
点评1:张工程师(某知名半导体公司滤波器设计专家)
"本文从基础理论到高阶优化,层层递进,尤其对MFB和状态变量滤波器的对比分析非常到位。建议补充一些实际调试技巧,比如如何用频谱仪快速校准滤波器参数。"
- 选择电容C₁=C₂=10nF(标准值)。
- 计算R₁、R₂、R₃:
- R₁ = Q / (2πf₀C₁G)
- R₂ = Q / (πf₀C₁)
- R₃ = Q / (πf₀C₁(2Q²-G))
(其中G为增益,通常设为1)
仿真验证:
使用LTspice或Multisim进行频响分析,确保-3dB带宽在200Hz左右(BW = f₀/Q = 1kHz/5 = 200Hz)。
解密有源带通滤波器:从基础到高阶设计实战
在现代电子电路中,**有源带通滤波器(Active Bandpass Filter)**扮演着至关重要的角色,广泛应用于通信系统、音频处理、医疗设备和信号检测等领域。与无源滤波器相比,它凭借运算放大器的增益特性,不仅能实现更精准的频率选择,还能有效抑制信号衰减。本文将深入剖析有源带通滤波器的工作原理、设计方法及实际应用,并探讨其优化策略。
相关问答